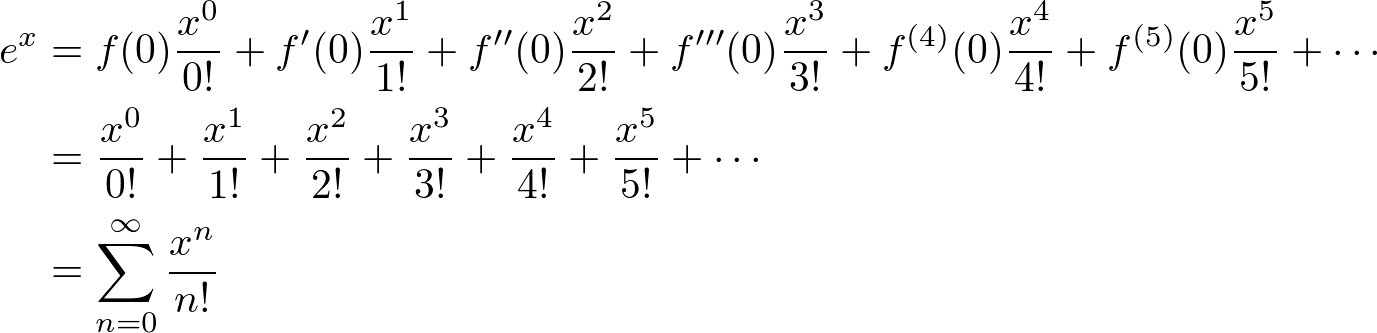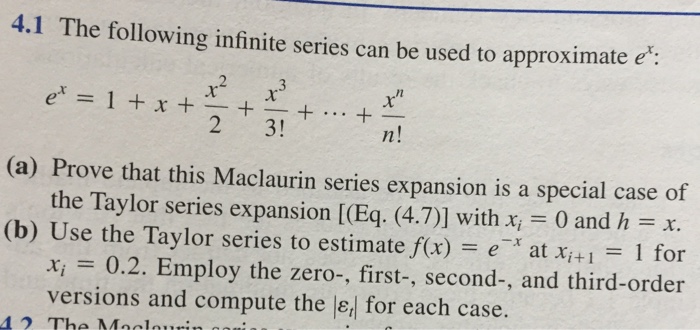E X Infinite Series

Stack exchange network consists of 176 q a communities including stack overflow the largest most trusted online community for developers to learn share their knowledge and build their careers. An infinite polynomial is called a power series. This important series converges to the number e the base of all continuously growing exponential functions.

d major scale piano finger position 2 octaves d major scale bass clef degree numbers d link router wifi password change d major scale notes guitar d major scale treble clef notes d major scale guitar notes d major chord guitar finger position d link router configurare

$Taylor Series Wikipedia$

Taylor Series Wikipedia

$Maclaurin Series Of Exponential Function$

Maclaurin Series Of Exponential Function

E X Taylor Expansion Where Do The Zeros Go Album On Imgur

Taylor Polynomial For E X About X 0 Youtube

$Taylor Series Wikipedia$

Taylor Series Wikipedia

Solved Question 3 30 Marks The Following Infinite Seri Chegg Com

Maclaurin series a maclaurin series is a special case of a taylor series where expansion is done about the point x 0 i e.

E x infinite series. X 5 5. Maclaurin series coefficients a k are always calculated using the formula where f is the given function and in this case is e x in step 1 we are only using this formula to calculate coefficients. In the above equation a 0. We consider the series expression for the exponential function.

That is you take the derivative term by term. In this setting e 0 1 and e x is invertible with inverse e x for any x in b. The derivative of e x. We found that all of them have the same value and that value is one.

Let s do that with the exponential function. X 4 4. The taylor series for e x e x 1 x x 2 2. The power series definition of the exponential function makes sense for square matrices for which the function is called the matrix exponential and more generally in any unital banach algebra b.

This first video clip is a quick introduction to the formula given above. Explanation of each step step 1. The neat thing about a power series is that to calculate its derivative you proceed just like you would with a polynomial. The mathematical constant e can be represented in a variety of ways as a real number since e is an irrational number see proof that e is irrational it cannot be represented as the quotient of two integers but it can be represented as a continued fraction using calculus e may also be represented as an infinite series infinite product or other sort of limit of a sequence.

A taylor series is an expansion of some function into an infinite sum of terms where each term has a larger exponent like x x 2 x 3 etc. In this table are the first few terms of one of the series shown above the one that represents f x e x with x 1. If xy yx then e x y e x e y but this identity can fail. Our first example from above is a geometric series.

The ratio between each term is and as promised we can show you why that series equals 1 using algebra. Some series converge to a finite limit and some diverge. X 3 3. When the ratio between each term and the next is a constant it is called a geometric series.