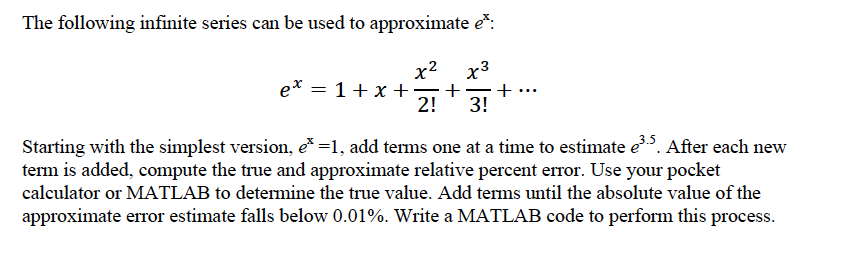E Infinite Series

Let left a n right be a sequence.

E infinite series. The ratio between each term is and as promised we can show you why that series equals 1 using algebra. To find approximations for special numbers like π and e. It is the base of the natural logarithm. We can differentiate or integrate term by term in our resulting series.

Apart from their uses in calculators and computers infinite series expansions are used. Taylor series a taylor series is an expansion of some function into an infinite sum of terms where each term has a larger exponent like x x 2 x 3 etc. Write a python program to compute the value of e 2 718281827 using infinite series. When the ratio between each term and the next is a constant it is called a geometric series.

Some series converge to a finite limit and some diverge. The taylor series for e x. The number e known as euler s number is a mathematical constant approximately equal to 2 71828 and can be characterized in many ways. In this table are the first few terms of one of the series shown above the one that represents f x e x with x 1.

To simplify some mathematical processes. It is the limit of 1 1 n n as n approaches infinity an expression that arises in the study of compound interest it can also be calculated as the sum of the infinite series. Python exercises practice and solution. This important series converges to the number e the base of all continuously growing exponential functions.

The mathematical constant e can be represented in a variety of ways as a real number since e is an irrational number see proof that e is irrational it cannot be represented as the quotient of two integers but it can be represented as a continued fraction using calculus e may also be represented as an infinite series infinite product or other sort of limit of a sequence. For an infinite series a 1 a 2 a 3 a quantity s n a 1 a 2 a n which involves adding only the first n terms is called a partial sum of the series.