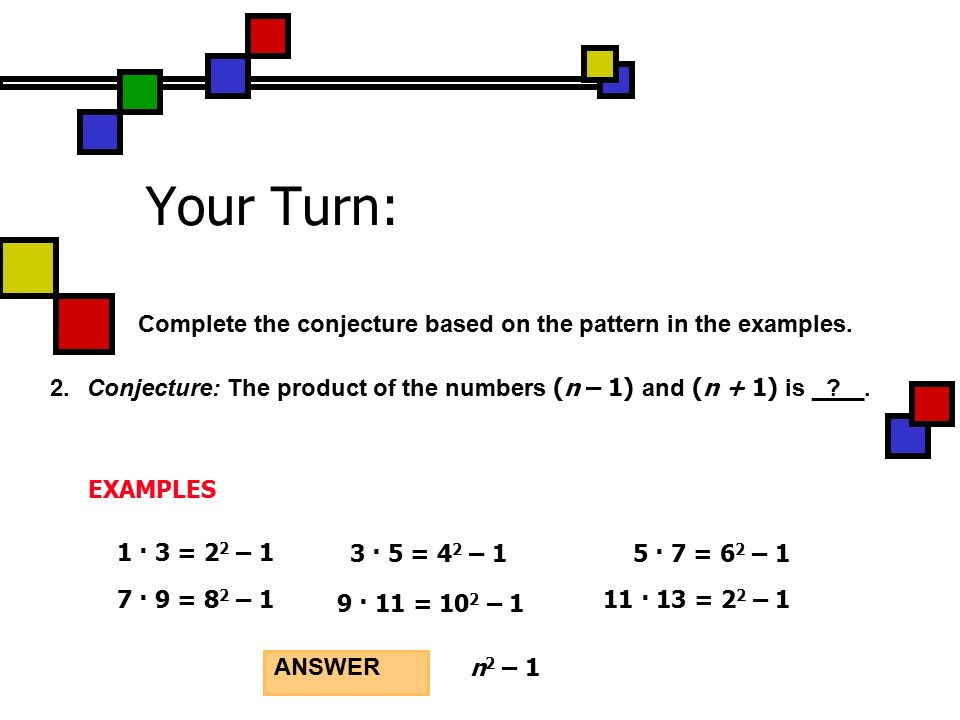
Conjecture 2 3 5 7 11

The primes up to 50 are 2 3 5 7 11 13 17 19 23 29 31 37 41 43 and 47. 8 3 5. As numbers get larger primes become less frequent and twin primes rarer still.

exatlon romania episodul 7 exatlon 20 mai 2018 expresor automat cafea boabe exatlon 5 februarie 2019 expatriates jobs in dammam exatlon 7 aprilie 2018 exatlon sezonul 1 episodul 1 exatlon 5 februarie 2018

What Is The Next Number In The Series 2 3 5 7 11 13 17 Quora

Solved A Prime Is An Integer That Can Only Divisible By 1 Chegg Com

Solved A Prime Is An Integer That Can Only Divisible By I Chegg Com

2 2 Patterns Inductive Reasoning Ppt Download

Gilbreath S Conjecture From Wolfram Mathworld

Inductive Reasoning Section 1 2 Objectives Use Inductive Reasoning To Make Conjectures Ppt Download

2 3 5 7 11 13 17 19 23 29.

Conjecture 2 3 5 7 11. In 1958 norman o. 2 3 5 7 11 13 17 19 etc. 100 3 97 or 11 89 or 17 83 or 29 71 or 41 59 or 47 53. 6 3 3.

10 5 5 or 3 7. Twin prime conjecture also known as polignac s conjecture in number theory assertion that there are infinitely many twin primes or pairs of primes that differ by 2. 4 2 2. Clearly all prime numbers other than 2 must be odd.

X 17 2 x 19 ans. A prime number is a positive integer which has exactly 2 positive integer factore one factor being 1 and the other factor is the positive number itself. The rest of the gaps are even numbers. 2 3 5 7 11 13 conjecture.

For example 3 and 5 5 and 7 11 and 13 and 17 and 19 are twin primes. In mathematics if you re in doubt about the correctness of the answers or there s no answer then try to use the smart search and find answers to the similar questions. Gilbreath was doodling on a napkin. The sequence of gaps the differences between each prime and the next is 1 2 2 4 2 4 2 4 6 2 6 4 2 and 4.

2 3 5 7 11 13 17 19 23 29 31 37 show that goldbach s conjecture is true for the even numbers from 20 to 40 by writing each number as a sum of two primes. He started by writing down the first few primes. The number 1 appears only once because all primes except for 2 are odd. By convention 1 is a not considered to be a prime number.

I ve illustrated the goldbach conjecture for some even numbers below. 42 is the next number in this sequence. Find an answer to your question 4. However the sequence 2 3 5 7 11 are the first five prime numbers.

So the next prime numbers after 11 are 13 then 17 19 23 29 31 37 41 43. So 1 2 3. Answer by jim thompson5910 35256 show source. Then 3 3 6 6 5 11 11 7 18 18 11 29.

This number sequence is adding the next prime number to the last number. 2 3 5 7 11 13 17 3 2 1 5 3 2 7 5 2 11 7 4 13 11 2 17 13 4 therefore the next number is obtained thus. 2 2 1 3 3 2 5 5 2 7 7 4 11 11 2 13 13 4 17 next term 17.